Hello!
You can find various explanations of how neural networks work on the Internet, but those that I came across were either too specific and aimed at specialists, or too simplified.
I tried to write my own explanations that would not be too simplified, but at the same time as clear as possible.
The article is 10 percent compiled from other articles, 30 percent compiled from many dialogues with different LLMs, and 60 percent “handwritten” based on articles and responses.
Content:
➤ Is it possible in describe in a few sentences how a neural network works?
➤ Why do LLM models give a question as input and output an answer, rather than a rephrased question?
➤ The data on which the LLM model is trained is becoming outdated, what are the possibilities for the model to generate relevant answers?
➤ How does the LLM model understand different languages?
➤ Input data:
➤ How RAG works
➤ Step 1: Tokenization (from text to tokens)
➤ Step 2: Token embedding (from token to vector)
➤ Product Quantization:
➤ Tensor
➤ Step 3: Positional Encoding / Embeddings:
➤ Step 4: Attention, Self-Attention (Attention Vector, Q,K,V-projections) and Attention Head Splitting (Multi-Head Attention)
➤ Step 5: Head Concatenation, Concatenated Multi-Head Attention
➤ Step 6: Output Projection (Wo)
➤ Step 7: Adding Residual
➤ Step 8: Layer Normalization
➤ Step 9: FFN (Feed-Forward Network) and MLP (Multilayer Perceptron)
➤ Step 10: Residual + LayerNorm (second normalization layer):
➤ Step 11: Feeding the block output to the next transformer block:
➤ Step 12: Final LayerNorm normalization after the last block:
➤ Step 13: Logits Projection + Softmax:
➤ Step 14: Selecting the next token (sampling):
➤ Intermediate samplers:
➤ Final samplers:
➤ Step 15. Iterate generation:
➤ Step 16. Converting tokens to words:
➤ TODO: there are many inaccuracies in the article, they will be corrected as soon as there is free time and desire
➤ Additional information:
➤ Launch methods (backends) for LLM models:
➤ Applications for running LLM models:
➤ LLM models storage format:
Interesting questions and answers:
➤ Is it possible in describe in a few sentences how a neural network works?
I’ll try. Imagine a structure consisting of hundreds of thousands of vectors in a space with thousands of dimensions. For each word, image segment, or any other entity, training results in a specific vector whose coordinates encode relationships with all other vectors in the space. This way, for all vectors of the query, one can compute their relationship to every other existing vector in the space. The vectors with the strongest relationships will be the answer.
➤ Why do LLM models give a question as input and output an answer, rather than a rephrased question?
The model is trained on “question → answer” texts, so when a question is presented, it does not generate the words of the question itself, but the most probable continuation — the answer.
During instructional learning (SFT) and RLHF, she is “rewarded” for useful answers, not for repeating the wording, so the parameters are biased towards answers.
In terms of probabilities: for a question, the probability of the next answer token is higher than the token repeating the question, and the decoder chooses it.
➤ The data on which the LLM model is trained is becoming outdated, what are the possibilities for the model to generate relevant answers?
Retrieval-Augmented Generation (RAG):
When a query is requested, the model searches for relevant documents in the current external database (search by vector or text index) and uses their context when generating a response. This way, you can get fresh information without overtraining the main network
Parameter-efficient retraining (LoRA, Adapters):
Instead of completely retraining the model, small adapters or low-rank matrices (LoRA) are built in, which are trained on new data. This allows you to quickly and inexpensively “teach” the model new facts or domains
I made a separate article about LoRA:
Model Editing:
Algorithms like MEMIT/ROME locally adjust the model weights to add or update specific facts without affecting the rest of the knowledge
Separate knowledge bases and graphs:
Instead of storing facts inside LLM parameters, move them to external KBs or knowledge graphs that are regularly updated, and the model only queries them for information
Integration with web search and API:
Connecting to real time via web browser plugins, third-party APIs, and search services (e.g. ChatGPT Plugins, Bing Search API) directly returns fresh content.
➤ How does the LLM model understand different languages?
The model “understands” different languages because during the training process it sees texts in many of them and learns to predict the next fragment regardless of the language. Key points:
Large multilingual corpus:
Texts (Wikipedia, books, web pages from Common Crawl, etc.) in dozens and hundreds of languages are collected for training. For example, the open BLOOM model had about 46 languages, and the share of each depends on the volume of available data
General subword tokenization:
Algorithms like BPE or SentencePiece are used, which break words into fragments (subword) and include symbols and sequences from different alphabets in the dictionary. So the model operates with a single set of tokens for all languages
Universal transformer architecture:
The same weights are used in the transformer when processing any language. Therefore, when training in different languages, the model finds common patterns (syntax, semantics) and uses cross-lingual transfer of knowledge
Not all languages and not in all volumes:
They train only in those languages where there is a sufficient volume of texts. Rare or low-resource languages are included in separate pretraining or receive a smaller share of data, so the quality of generation on them is lower
Special pretraining and adapters:
To improve knowledge of little-known languages, continuous pretraining is used on local data or adapters (LoRA) are inserted, which fine-tune the model’s knowledge for a specific language.
➤ Input data:
At the input, the neural network receives incoming data in the form of a user request. General information is also added to the user’s request, which allows for a more accurate answer. If the neural network supports RAG (Retrieval-Augmented Generation), then the following are also added to the request:
- Data from the vector database, if it was previously added what is needed to generate a more relevant response
- Extracted from an Internet page or document – in order to reduce their size, a specialized embedding neural network is often used, it finds all the appropriate pieces of text and adds them to the context of the request
Example of neural network embedding settings for the Page Assist Chrome extension
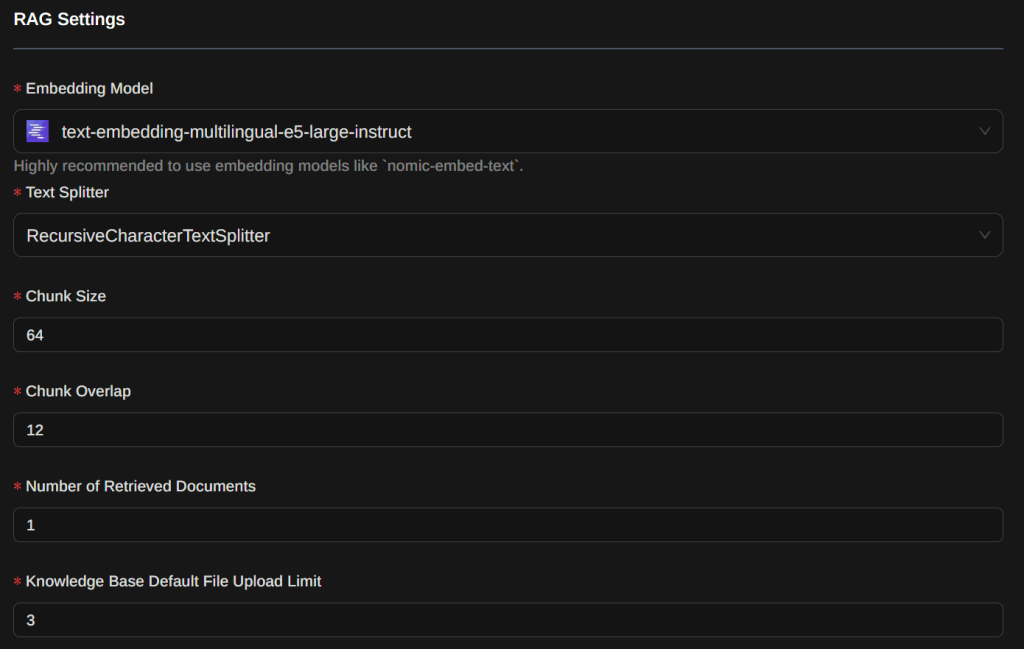
➤ How RAG works
The system consists of two main components
Retrieval:
Searches for relevant information from an external knowledge base (usually a vector base, such as FAISS, Qdrant, Weaviate). This base is usually built in advance from text documents (pdf, markdown, html, etc.) transformed into embeddings using a model (e.g. BERT, Instructor, or SentenceTransformer).
Generation:
LLM (GPT, LLaMA, Mistral, etc.) receives the original query + the documents found and generates the final response.
Some neural networks use markup to separate the user’s query, the context obtained using RAG, and the general message.
Example:
context:
this is data obtained from the Internet using an embedding neural network or from a vector storage and sorted by score matches in descending order
{
"context": [
"Penicillin is the first antibiotic discovered, produced from a mold fungus of the genus Penicillium. It is used to treat bacterial infections such as sore throat, syphilis, and pneumonia. Penicillin destroys the cell wall of bacteria, causing them to die.",
"Some people are allergic to penicillin. This can cause serious reactions, including anaphylaxis, so it is important to check for allergies before prescribing the drug."
],
"instructions": "Answer in simple terms, using only information from the context. If there is no answer, write 'Information not found'.",
"question": "What is penicillin and what is it used for?"
}Steps of the neural network:
➤ Step 1: Tokenization (from text to tokens):
LLM doesn’t work with words directly — it works with tokens (parts of words or characters) converted to numbers.
Example:
User text: "Hello, world" Token ID in the model dictionary for the word: "Hello" = 1123 "," = 15 "world" = 345 Get an array of token IDs: ["Hello", ", ", ", "world"] = [1123, 15, 345]
How it’s achieved:
An algorithm like Byte Pair Encoding (BPE), Unigram, WordPiece or SentencePiece is used.
BPE tokenizer finds the most frequent pairs of characters.
WordPiece builds tokens based on the probability of hierarchical partitions.
Often tokens are not individual words, but parts of words.
The dictionary includes special markers for the beginning of a word (space, “##”, etc.), so no subtoken crosses the boundary of two words.
Tokenization is always “greedy” — the longest token that matches the beginning of the remaining line is taken.
Example:
Users text:
"unbelievable"
Token IDs in the models vocabulary for parts of the word:
"un" = 24
"believ" = 126
"able" = 36
Resulting array of token IDs:
["un", "believ", "able"] = [24, 126, 36]
Or a shorter variant:
("un", "bel", "##ievable")Different words with different meanings can share common tokens — for example, “unhappy” and “unfold” both contain the token “un”:
Although “un” appears in both words, the model doesn’t just look at this fragment alone — it immediately considers the surrounding tokens and the entire phrase (more on that later in the article).
First, “un” is turned into a vector — just a set of numbers describing this part of the word.
Then, the transformer (a multi-layer neural network) mixes this vector with the vectors of neighboring tokens (“happy” or “fold”) and adds information about their positions in the sentence.
As a result, in the first layer, “un” in “unhappy” is already different from “un” in “unfold” because the surrounding context is different.
In other words, the shared fragment “un” is neutral on its own, and the actual meaning is formed layer by layer based on the context.
Why tokens and not words:
Smaller dictionary = saves memory.
Rare and compound words are processed better.
Allows the model to “learn” to understand the structure of words.
The vocabulary size, or “vocab_size,” determines how many unique tokens the model can handle.
A larger vocabulary = fewer word splits, but a larger embedding layer.
The word “programming” can be a single token in a model with a large vocabulary,
or it can be split into parts (“pr,” “ogram,” “miration”) in a model with a smaller vocabulary.
Vocab sizes of popular models:
Model | Dictionary size| -----------------------|----------------| LLaMA 1/2 | 32 000 | LLaMA 3 | 128 000 | Gemini 1.0/1.5 | ~4 МБ | Gemma 1/2 | 256 000 | Gemma 3 | 262 000 | Qwen 1.5 | 151 936 | Qwen 2 | 152 064 | Qwen 2.5 | 152 064 | DeepSeek LLM | 102 400 | DeepSeek-Coder | 32 256 | DeepSeek V2/V3 | 102 400 | DeepSeek-R1 | 129 280 |
Image tokenization:
Unlike text tokenization (where tokens are words, subwords, symbols), in images tokens are image fragments or feature representations. The main approaches are discussed below.
For images, instead of tokens, a matrix (or tensor) of pixels is obtained immediately.
In classic convolutional networks (CNN), small image patches (e.g. 3×3 or 5×5 pixels) are slid across the image, and for each patch, a convolution with a set of filters produces a feature vector. These vectors are collected into feature maps and passed on.
In modern image transformers (Vision Transformer), the image is divided into “patches” (squares, say, 16×16 pixels), each patch is aligned into a vector and also projected through the embedding matrix into a vector representation, like a token in NLP.
The main methods of image tokenization:
Patch Embedding (splitting into patches) is a classic ViT approach:
The image is divided into a grid of square patches, for example, 16×16 pixels.
Each patch is flattened into a vector, then linearly projected onto an embedding of fixed dimension (e.g. 768).
The result is a sequence of tokens: one token per patch.
Example:
224×224 RGB image with 16×16 patches → 14×14 = 196 tokens + [CLS] token.
Each token: a vector of size 768.
CNN Feature Maps as tokens:
Convolutional networks (ResNet, ConvNext) are used to extract features.
Spatial features (feature map) can be interpreted as tokens at the output, where each grid element is a vector.
Used in CLIP and other hybrid models.
VQ-VAE / VQ-GAN tokenization (discrete):
The encoder converts the image into a feature map and then quantizes it into discrete tokens (indices from a dictionary).
Each token is an index into a dictionary of visual patches.
Used in DALL E, Imagen, LLaVA and other multimodal generative models.
Pros: the model works with “words” of the visual language.
Cons: loss of accuracy, unstable generation.
Segment/Region-based tokens (DETR, Region Attention):
The image is divided into semantic regions (segmentation, objects).
Each region is transformed into a token using feature aggregation.
Used in object detection and visual question answering (VQA) tasks.
Patch + Positional Encoding:
As in NLP, each patch is supplemented with positional information (absolute, relative or learnable) to preserve the spatial structure of the image.
Maximum context length:
Context is the working memory of the model, the context size is the maximum number of tokens (words, characters or parts of them) that the language model can process in one request.
This is the “amount of memory” that the model can see at one time to form a response. Anything beyond this window is forgotten or not seen directly by the model.
The size of the context directly affects the model’s ability to remember previous messages in the conversation.
The model does not have built-in long-term memory – it does not “remember” you as a person. It simply processes the entire previous conversation as input text (tokens) passed with each request. This is called context.
Maximum context length of popular models:
| Model | Maximum context length | |-------------------------|------------------------------| | LLaMA 1/2 |2 048 / 4 096 | | LLaMA 3 |8 192 | | Gemma 1/2 |8 192 | | Gemma 3 |128 000 | | Qwen 1.5 |32 768 | | Qwen 2 |32 768 | | Qwen 2.5 |131 072 | | DeepSeek LLM |4 096 | | DeepSeek-Coder |16 384 | | DeepSeek V2/V3 |128 000 | | DeepSeek-R1 |131 072 | | Gemini 1.0/1.5 |32 768 / 1 000 000 |
➤ Step 2: Token embedding (from token to vector):
In the LLM model, for each token ID, a Token Embedding, or array of numbers, is stored. These numbers describe what that token means, as if you were translating a word into mathematical form.
Token embedding initially has a fixed value for each token, but then gets refined as it goes through the layers.
As Token Embedding goes through multiple layers of the transformer, it becomes contextualized: it takes into account the meaning of the entire phrase. The output is a vector that contains the “meaning” of the word in context.
Vector size (Embedding Size, d_model):
The number of dimensions in token embedding is fixed for the entire model and depends on its architecture.
Example:
User text: "Hello" Token ID in model dictionary for word: "Hello" = 1123 Token embedding for token ID 1123 = array of float values with d_model= 4096 elements: [0.034, 0.120, 0.905, ..., 0.028]
Popular models embedding size (d_model):
Model | d_model | -----------------------|---------| LLaMA 1 (7B) | 4096 | LLaMA 2 (13B) | 5120 | LLaMA 2 (70B) | 8192 | LLaMA 3 (8B) | 4096 | LLaMA 3 (70B) | 8192 | Gemini 1.0 Pro | 6144 | Gemini 1.0 Ultra | 8192 | Gemini 1.5 Pro | 8192 | Gemma 1 (2B) | 2048 | Gemma 1 (7B) | 3072 | Gemma 2 (9B) | 4096 | Gemma 2 (27B) | 6144 | Gemma 3 (12B) | 5120 | Gemma 3 (27B) | 8192 | Qwen 1.5 (7B) | 4096 | Qwen 2 (7B) | 4096 | Qwen 2.5 (7B) | 4096 | DeepSeek LLM (7B) | 4096 | DeepSeek LLM (67B) | 8192 | DeepSeek-Coder (6.7B) | 4096 | DeepSeek-Coder (33B) | 8192 | DeepSeek-R1 | 8192 |
The number of elements of the meaning vector affects:
Higher dimensionality = more “space” for storing semantics, syntax, context.
This allows us to distinguish more subtle meanings between tokens.
The memory size of all weights and activations grows quadratically with embedding size.
embedding size = d_model = 4096 takes up 4 times more memory than embedding size = d_model = 2048
Vector precision:
Also, the floating-point numbers that make up the vector can have different precision:
Lower precision reduces the size of the model and speeds up processing.
Usually, models are trained at full FP32 precision (float32), that is, the vector consists of 32-bit numbers.
Quantization:
Quantization is used to reduce precision and make the model lighter — the process of converting floating-point numbers (e.g. FP32) into more compact integer representations (e.g. INT8), while preserving the approximate value.
This introduces a small loss of precision, but it often does not critically affect the output quality.
Format: FP32 (float32), 32 bits = 4 bytes Purpose: Full precision. Used for training models, as well as for precise inference. Provides maximum precision, but requires a lot of memory and computing resources. Binary value: 01000000 01001001 00001111 11011011 Actual value: 3.14159 Possible quantization types: Not used - this is the full (not quantized) format. Format: FP16 (float16), 16 bits = 2 bytes Purpose: Half precision. Used for accelerated training and inference on GPUs (e.g. NVIDIA Tensor Cores). Faster and 2x more memory efficient than FP32. Binary value: 01000000 10010000 Actual value: ≈ 3.1406 Possible quantization types: QFloat16 (if adaptive mixing in mixed precision is used). Format: BF16 (bfloat16), 16 bits = 2 bytes Purpose: Alternative to FP16, used in TPU and some GPUs. Has the same exponent as FP32, but a shortened mantissa. Faster and more compact, while maintaining the range of FP32. Binary value: 01000000 10010000 Actual value: ≈ 3.140625 Possible quantization types: QBFloat16 (rarely used directly, but seen in TPU inference). Format: INT8 (8 bits), scale = 0.125 Purpose: Quantized integer. Used in optimized models for inference on CPU and mobile devices. Requires scale and offset (zero_point) restoration. Quantized value: 25 Binary value: 00011001 Actual value: 25 × 0.125 = 3.125 Possible quantization types: Q8_0, Q8_1, Int8Affine, PerChannelQuant (ONNX), dynamic/int8 (TensorFlow Lite) Format: INT4 (Q4), 4 bits, scale = 0.5 (2 numbers in 1 byte) Purpose: Very compressed format for language models. Used in llama.cpp, GGUF and other systems. Provides significant reduction in model size. Requires reconstruction (dequantization) at startup. Quantized value: 7 (maximum value for signed 4-bit int: -8…+7) Binary value: 0111 Actual value: 7 × 0.5 = 3.5 Possible quantization types: Q4_0, Q4_1, Q4_K, Q4_G, Q4_M (llama.cpp, GGUF) Format: INT2 (Q2), 2 bits, scale = 1.0 (4 numbers in 1 byte) Purpose: Extremely compressed format for use in LLM on devices with limited resources. Used in some variants of GGUF, MLC, and in experiments with extreme quantization. Quantized value: 1 (maximum values: -2…+1) Binary value: 01 Actual value: 1 × 1.0 = 1.0 Possible quantization types: Q2_K (llama.cpp, GGUF) Format: INT1 (Q1), 1 bit, scale = 2.0 (8 numbers in 1 byte) Purpose: Minimum possible precision. Used in binary neural networks and prototypes. Usually values are -1 or +1. Rarely used in LLM, but can be useful in BNN (Binary Neural Networks). Quantized value: 1 Binary value: 1 Actual value: 1 × 2.0 = 2.0 Possible quantization types: Q1, BinaryNet, XNOR-Net (usually in academic/experimental BNNs)
Models can also have additional quantization parameters:
_K - Denotes "K-Block" quantization. - Weights are split into blocks of fixed length (e.g. 32 or 64 values). - Within each block, a common scale and zero_point are used. - This allows for a significant reduction in model size while maintaining higher accuracy compared to simple quantization. - Example formats: Q2_K, Q4_K, Q6_K, Q8_K _0, _1 - Indicate which quantization scheme is used: - _0: basic scheme, no bias, one scale per block - _1: improved scheme, with additional bias or scale shifts - Used in formats: Q4_0, Q4_1, Q5_0, Q5_1, Q8_0, Q8_1 - As a rule, _1 provides better accuracy with a slight increase in size Compression/precision level labels: K_L, K_M, K_S, K_G K_L - Kvantization Low - Low model size, minimal accuracy - Suitable for devices with extremely limited resources - Maximum aggressive quantization K_M - Kvantization Medium - Medium trade-off between accuracy and size - Suitable for most local tasks K_S - Kvantization Small - The model is maximally compressed in size, even at the expense of quality - Often used as a reference for extreme compression K_G - Kvantization General - Balanced model: reasonable compromise between speed, quality and size - Works well on most CPUs Example of the model name: "mistral-7b.Q4_K_M.gguf" — this means: - Mistral 7B model - Q4_K (4-bit K-block) quantization is used - Compromise level: Medium
➤ Product Quantization:
A method that allows you to strongly compress feature vectors (embeddings) by breaking them into parts and encoding each part through the closest template (cluster).
How it works:
There is a vector (for example, 128 numbers in size). This can be a text or image embedding from a neural network.
We break the vector into pieces – for example, 8 parts with 16 numbers (128 / 8 = 16).
For each position of the piece, we train our own encoder (quantizer) – on big data, we select in advance which “templates” (cluster centers) are similar to possible pieces.
For example:
the first piece can be similar to template #12,
the second – to template #3,
the third – to template #88,
and so on.
We save only the numbers of these templates. Instead of storing 128 numbers (float32 = 512 bytes), we store, for example, 8 numbers (1 byte per pattern) – 8 bytes in total.
QAT (Quantization-Aware Training) quantization:
is a method of quantization of neural networks, in which quantization is taken into account already during model training. It allows to achieve almost the same accuracy as the original model with float parameters, while the model will use more compact int8 or other low-bit formats suitable for efficient execution on devices with limited resources (for example, smartphones or microcontrollers).
How QAT works – step by step:
Model in float32:
Training starts with a regular model using floating-point numbers (usually float32). This ensures high accuracy and stability of training.
Quantization imitation during forward pass (fake quantization):
At each forward pass, the values (weights, activations) are emulated as quantized, i.e. they are converted to int8 and then back to float32. This allows the model to “see” quantization errors already at the training stage.
float32 → int8 → float32
Thus, during backpropagation, gradients are calculated using the float32 version, but errors due to quantization still affect training.
Backward pass:
Gradients are calculated as usual, but taking into account distortions from fake quantization. This allows the model to adapt to the fact that the weights and activations will be used in low precision later.
Exporting the final model to int8:
Once training is complete, the weights are indeed quantized to int8, and the model can be compiled and run in production.
What exactly is quantized:
Weights are float32 → int8
Activations are float32 → int8
(Sometimes gradients and intermediate states are also quantized, but this is rare.)
Why use QAT:
Above accuracy than post-training quantization (PTQ)
Low memory consumption
Faster execution on CPU/GPU/NPUs with int8 support
Especially important for mobile and embedded devices (e.g. Android)
Then the model is sent to the transformer.
Transformer:
The neural network architecture that became the basis for modern language models such as ChatGPT, BERT, LLaMA, Gemma and many others.
It was first described in a 2017 scientific paper called “Attention is All You Need”.
Simply put, a transformer is a “smart machine” that can read and understand text by processing all words at once, rather than one at a time, as previous models (e.g. RNN, LSTM) did.
Transformer Layers:
these are repeating blocks that each token within the model passes through.
One layer (or “transformer block”) includes:
Self-Attention:
a token “looks” at other tokens and decides who is important.
Feed-Forward Network:
refining and transforming each token.
Layer Normalization or LayerNorm:
stabilizing computation.
Residual Connections:
so that the model does not “forget” the initial information.
LayerNorm can be before or after Residual (Pre-LN vs Post-LN).
and other stages.
Each layer of the transformer (Transformer Block) is a separate set of parameters that:
are independently trained,
are independently applied to the input data,
provide an increasingly “deeper” understanding of the meaning and context.
What does “32 layers” mean:
each token goes through 32 such operations, one after another, after each layer the token becomes more and more informed, i.e. its representation (vector) reflects the context more and more deeply
Number of model layers (transformer layers):
| Model | Number of layers | |-----------------------|------------------| | LLaMA 1 (7B) | 32 | | LLaMA 2 (7B) | 32 | | LLaMA 2 (13B) | 40 | | LLaMA 2 (70B) | 80 | | LLaMA 3 (8B) | 32 | | LLaMA 3 (70B) | 80 | | Gemini 1.0 Pro | 32 | | Gemini 1.0 Ultra | 64 | | Gemini 1.5 Pro | 64 | | Gemma 1 (2B) | 18 | | Gemma 1 (7B) | 28 | | Gemma 2 (9B) | 32 | | Gemma 2 (27B) | 40 | | Gemma 3 (12B) | 36 | | Gemma 3 (27B) | 48 | | Qwen 1.5 (7B) | 32 | | Qwen 2 (7B) | 28 | | Qwen 2.5 (7B) | 28 | | DeepSeek LLM (7B) | 30 | | DeepSeek LLM (67B) | 95 | | DeepSeek-Coder (6.7B) | 32 | | DeepSeek-Coder (33B) | 64 | | DeepSeek-R1 | 95 |
Activation:
these are the intermediate outputs of the neural network after applying functions and layers).
We can say that activations are data that “live inside the network” at each stage of the input passing through model.
➤ Tensor:
in a neural network, this is a multidimensional array of numbers that the model layers work with.
Input data:
Text → tokens → embeddings → tensor batch_size × seq_len × embedding_dim.
Model weights:
The weight matrices in the layers are also tensors.
Intermediate representations (activations):
The output of each layer (e.g. LayerNorm, Attention) is a tensor.
Gradients:
During training, the model calculates gradients (tensors) to update the weights.
➤ Step 3: Positional Encoding / Embeddings:
Without additional information, the phrases:
“The cat eats fish”
“The cat eats fish”
could be perceived the same, because the set of words is the same.
To give the model a sense of order, each token (word or part of a word) is added a position vector – a set of numbers that tells the model what positions the words are in.
Token embedding + Positional Encoding / Embeddings = Total vector
Positional Encoding / Embedding is:
A vector of the same dimension as the token (d)
Represents a position in a sequence
Can be given by a formula (sin/cos) or trainable
Combined with the token vector at the input to the model
Which type is used in models:
| Method | Model/Family | Description | |-----------------------------|------------------------------------|----------------------------------------| | Sinusoidal Encoding | Transformer | Untrained, based on sines and | | | (Vaswani et al., 2017) | cosines with different frequencies | |-----------------------------|------------------------------------|----------------------------------------| | Learnable Embeddings | BERT, GPT-2, | Learnable position table, similar to | | | DistilBERT, ELECTRA | word embeddings | |-----------------------------|------------------------------------|----------------------------------------| | Rotary Positional Embedding | GPT-NeoX, LLaMA, LLaMA 2/3, | Vector rotation - preserves relative | | (RoPE) | ChatGLM, Mistral | positions between tokens | |-----------------------------|------------------------------------|----------------------------------------| | ALiBi | OPT, BLOOM, Phi-2 | Linear bias, added to attention score, | | | | does not require storing positions | |-----------------------------|------------------------------------|----------------------------------------| | Relative Position Bias | T5, DeBERTa, Transformer-XL, | Uses offsets between tokens instead of | | | Pegasus, LongT5 | absolute positions |
Example:
User text: "Hello, world" Token ID in model dictionary for word: "Hello" = 1123 "," = 15 "world" = 345 Get array of token IDs: ["Hello", ",", "world"] = [1123, 15, 345] Token embedding from model base for: Token ID 1123 = [0.034, 0.120, 0.905, ..., 0.028] Token ID 15 = [0.022, -0.010, -0.313, ..., 0.117] Token ID 345 = [-0.102, 0.241, 0.543, ..., 0.055] Position of word token ID in user text: [1123, 15, 345] = [position 0, position 1, position 2] Calculate or obtain from the model base the position vector: Position vector 0 = [0.001, 0.087, -0.432, ..., 0.019] Position vector 1 = [0.005, -0.013, 0.021, ..., -0.012] Position vector 2 = [-0.003, 0.099, -0.082, ..., 0.003] Summary vector for ID 1123: Token embedding [0.034, 0.120, 0.905, ..., 0.028] + Position vector 0 [0.001, 0.087, -0.432, ..., 0.019] = [0.035, 0.207, 0.473, ..., 0.047] similarly for other tokens
Calculating Sinusoidal Position Encoding:
Sine position encoding is used in Transformer models to provide information about the position of tokens in the input sequence. Unlike recurrent networks, Transformer does not have a built-in mechanism for taking into account the order of tokens. Therefore, it is necessary to explicitly encode information about the position of each token.
From a mathematical point of view:
pos - token position in the sequence (starting with 0) i - index of the positional encoding vector dimension (starting with 0) d_model - positional encoding vector dimension (embedding dimension) PE(pos, i) - i-th element of the positional encoding vector for position pos. 10000 is a hyperparameter. It is used to scale the position and frequency of the sinusoids. Choosing this value allows the model to easily extrapolate to sequences longer than the ones it was trained on. Then the i-th element of the position encoding vector for position pos: PE(pos, 2i) = sin(pos / 10000^(2i/d_model)) PE(pos, 2i+1) = cos(pos / 10000^(2i/d_model))
The formula uses different frequencies (wavelengths) of the sinusoidal functions for different dimensions of the position encoding vector.
Even dimensions use sine, and odd dimensions use cosine. This allows the model to distinguish positions at different phases and amplitudes.
Dividing pos by 10000^(2i/d_model) reduces the frequency of the sinusoid as the dimension index i increases.
This creates slower oscillations for higher dimensions, allowing the model to distinguish positions at different scales.
Example:
pos = 0 (first token) d_model = 4 (position encoding vector dimension) Then the position encoding vector encoding PE(0) will have dimension 4. Let's calculate each element: i = 0: PE(0, 0) = sin(0 / 10000^(2*0/4)) = sin(0) = 0 PE(0, 1) = cos(0 / 10000^(2*0/4)) = cos(0) = 1 i = 1: PE(0, 2) = sin(0 / 10000^(2*1/4)) = sin(0) = 0 PE(0, 3) = cos(0 / 10000^(2*1/4)) = cos(0) = 1 PE(0) = [0, 1, 0, 1] Now let's calculate the positional encoding vector for pos = 1: i = 0: PE(1, 0) = sin(1 / 10000^(2*0/4)) = sin(1) ≈ 0.8415 PE(1, 1) = cos(1 / 10000^(2*0/4)) = cos(1) ≈ 0.5403 i = 1: PE(1, 2) = sin(1 / 10000^(2*1/4)) = sin(0.01) ≈ 0.01 PE(1, 3) = cos(1 / 10000^(2*1/4)) = cos(0.01) ≈ 1 PE(1) = [0.8415, 0.5403, 0.01, 1]
Important:
In real Transformer models, the positional encoding is usually computed for all possible positions in the sequence in advance and stored as a table.
Then, when fed with an input sequence, the corresponding positional encoding vectors are added to the token embeddings.
The choice of the hyperparameter 10000 is empirical and can be tuned depending on the specific task.
Relative positional offsets:
Instead of encoding the absolute position of each token, some Transformer variants introduce relative positional offsets. This allows the model to directly take into account the distance (and direction) between pairs of tokens, rather than their “global” position in the sequence.
Why relative offsets are needed:
When generating or processing long texts, it is important how far apart words are, and not just their absolute indices.
Absolute embeddings do not generalize well to longer sequences than those on which the model was trained.
Relative offsets provide greater flexibility: the model learns, for example, “that there can be an action object 3 positions to the right”, regardless of where this sentence is in the text.
Transformer-XL, relative positions via key offsets and queries:
In classic self-attention we calculate:
score_{i,j} = (Q_i · K_j) / sqrt(d_k)
In Transformer-XL, two additional sets of embeddings are introduced:
E^R[r] — embedding for the relative shift r = j - i
U, V — two shift vectors
Final formula:
Q_i · E^R[j-i] - content-dependent part of attention, taking into account the relative shift
V · E^R[j-i] - content-independent part, defining the basic bias for a given offsets
score_{i,j} = (1/√d_k) * (Q_i K_j + Q_i E^R[j-i] + U K_j + V E^R[j-i])➤ Step 4: Attention, Self-Attention (Attention Vector, Q,K,V-projections) and Attention Head Splitting (Multi-Head Attention)
Now that tokens have not only “meaning” but also “position,” they go through a self-attention mechanism, where each word looks at the other words to decide which one I should pay attention to in order to better understand its meaning.
This is similar to how a person reads a sentence: they can go back to previous words with their eyes to get the context right.
Self-Attention is responsible for understanding the context — which tokens are important to each other, and allows each token to look at all the others in a balanced way sequences and determine what to look for when constructing meaning.
Softmax:
This is a function that takes a vector of numbers as input and turns it into a probability distribution where all values are non-negative and sum to 1.
softmax(zᵢ) = exp(zᵢ) / ∑ⱼ exp(zⱼ)
The model creates three representations for each token:
Q (question): what am I looking for?
K (key): what can I offer?
V (value): what information do I bring?
Each word compares its Q to the K of all the other words to know which one to look at. After that, it collects the necessary information from the V words that turned out to be important.
To calculate the representations, the layer weight matrix is used – this is the learning parameter of the neural network, that is, it is initialized randomly when the model is created and is trained along with the other weights. Initially random, then it becomes “smart” due to training.
How they are trained:
During the backpropagation stage, the model compares its predictions with the correct answer (e.g. the next token) and updates Wq, Wk, Wv along the error gradient using an optimizer (e.g. Adam).
The parameters Wq, Wk, and Wv can be common or different for each head, depending on the model.
Wq (Query Projection):
Creates a “question” — what the token wants to find in other tokens.
Determines the direction of attention.
Token Q = Token X total vector * Layer weight Wq
Wk (Key Projection):
Creates a “key” — what each token offers to the others.
Used for comparison with Q (how “similar” is Qᵢ to Kⱼ).
Token K = Token Sum Vector X * Layer Weight Wk
Wv (Value Projection):
Creates the “information” that a token can convey if it has been noticed.
Token V = Total vector of token X * Weight of layer Wv
Attention-head:
Models also have an attention-head. Each attention-head processes the input vector in its own way, through its Q, K, V projections, and looks at different aspects of the sentence.
Each attention-head has its own point of view:
one head can track grammar (for example, subject and predicate),
another — semantic connections (for example, who acts on what),
a third — positions, context, etc.
Instead of one “point of view” — several at once.
Each head sees the entire text, but — analyzes it in its own way, through projection and attention.
Example:
In the sentence
“The boy who held the ball ran away.”
Different heads can see
Head 1: “boy” ↔ “ran away” → who performs the action
Head 2: “which” ↔ “held” → nested grammatical relation
Head 3: “ball” ↔ “held” → object of the action
Each head produces its own representation for each token, taking into account its “observations.”
Multi-Head Attention Architecture (MHA):
Classical self-attention implementation, as in original article “Attention is All You Need”.
What’s going on:
There are multiple heads
Each head has its own Wq, Wk, Wv
Each head analyzes the entire context in its own way
The results of all heads are combined and passed through a common Wo
Pros:
Flexible: each head “looks” at the input in its own way
Works great with large computing resources
Cons:
Very expensive in memory and speed with a large number of heads
Especially with long sequences
Multi-Query Attention Architecture (MQA):
An optimized version of attention used in GPT-3.5, PaLM, Gemma and others to reduce memory load and speed up inference.
What’s going on:
One Wq per head
Only one Wk and one Wv
All heads share the same keys and values
Pros:
Less memory: K and V are stored in a single instance
Faster generation: less data is stored between steps
Cons:
Less flexibility (all heads “look at” the same K and V)
May slightly degrade quality on complex tasks
Grouped Query Attention (GQA) architecture:
a combination of the previous 2 approaches
Example:
For example, the Gemma 3 neural network architecture uses Grouped Query Attention (GQA), a compromise between the standard Multi-Head Attention (MHA) and Multi-Query Attention (MQA). In this scheme, the Wq (for queries) matrices are different for each head, while the Wk (for keys) and Wv (for values) matrices can be shared across groups of heads.
In this neural network:
Wq: Each head has its own unique Wq matrix, allowing each head to focus on different aspects of the input sequence.
Wk and Wv: Heads are divided into groups, and within each group, a common Wk and Wv matrix is used. This reduces the amount of computation and memory required to store keys and values.
This means that the 8 query heads (Wq) are divided into 4 groups, each of which shares the same key and value matrices (Wk and Wv).
As a result, a Gemma 3 model of size 27B has
80 layers and 64 heads, inside which there will be:
64 different Wq (Query Projection)
8 different Wk (Key Projection)
8 different Wv (Value Projection)
64 different Wo (Output Projection)
80 MLPs with different weights (Feed-Forward Network)
80 LayerNorms with different gamma/beta parameters
Number of attention heads of popular models:
| Model | Number of attention heads | |-------------------------|------------------------| | LLaMA 1/2 | 32 | | LLaMA 3 | 32 / 64 / 128 | | Gemma 1/2 | 16 | | Gemma 3 | 8 | | Qwen 1.5 | 40 (Q) / 8 (KV) | | Qwen 2 | 40 (Q) / 8 (KV) | | Qwen 2.5 | 40 (Q) / 8 (KV) | | DeepSeek LLM | 32 (7B) / GQA (67B) | | DeepSeek-Coder | 16 / 32 / 56 | | DeepSeek V2/V3 | 128 | | DeepSeek-R1 | 128 |
Causal Masking:
used in some models. When a language model (LLM) generates text, it must predict the next word based only on the previous words.
This means that a Token should not have access to the tokens that come after it.
To enforce this restriction, causal masking is used – this is a mechanism that “prohibits” attention from seeing future tokens.
How it works:
In regular self-attention, each token “looks” at all tokens in the sequence, including future ones.
This is unacceptable during generation, because it would be “cheating” — the model sees the answer in advance.
To prevent this, a mask is used when calculating attention — a special matrix called an attention mask.
For a sequence of length n, a triangular mask is created in which:
Values above the diagonal are replaced with -∞ or a large negative number.
After that, softmax is applied, and these values turn into zero attention.
Example mask (for n = 4 tokens): [ [0, -∞, -∞, -∞], [0, 0, -∞, -∞], [0, 0, 0, -∞], [0, 0, 0, 0] ] This means: Token 0 sees only itself. Token 1 sees itself and token 0. Token 2 sees itself, token 1, and token 0. Token 3 sees everything before it.
Where Causal Masking is used:
GPT, LLaMA, Mistral, Gemma and other autogenerative models necessarily use causal masking.
BERT, on the contrary, uses bidirectional attention – the token can see the entire context (including the future), because the task is different – not generation, but understanding.
Why is this important, without causal masking:
The model with training will “peek” at the correct answer (the next token).
This will lead to poor generation when using the model in inference, when the future is unknown.
The role of position in Self-Attention:
Without Position Encoding, Self-Attention only sees the meaning of words, but not their order. With Position Encoding added, Self-Attention starts to take into account not only what is written, but also where it is:
“Boy” used to “read” → he is probably a subject
“Book” next to “read” → most likely an object
What the transformer does in the end:
Each word gets information about its position
Through self-attention, each word “asks” all the others:
“What do you mean to me in this context?”
The model adds these answers together and gets a deep understanding of the meaning of the entire phrase
Repeats this on each layer (usually 12-40 times), deepening the “understanding”
User text: "Hello, world" Token ID from the model dictionary: "Hello" = 1123 "," = 15 "world" = 345 Getting an array of token IDs: ["Hello", ",", "world"] = [1123, 15, 345] Token embedding or attention vector from the model base: "Hello" = ID 1123 = [0.034, 0.120, 0.905, ..., 0.028] "," = ID 15 = [0.022, -0.010, -0.313, ..., 0.117] "world" = ID 345 = [-0.102, 0.241, 0.543, ..., 0.055] Calculate or obtain the position vector from the model base: Position vector "Hello" = [0.001, 0.087, -0.432, ..., 0.019] Position vector "," = [0.005, -0.013, 0.021, ..., -0.012] Position vector "world" = [-0.003, 0.099, -0.082, ..., 0.003] For "Hello": Token embedding [0.034, 0.120, 0.905, ..., 0.028] + Position vector [0.001, 0.087, -0.432, ..., 0.019] = Sum vector X [0.035, 0.207, 0.473, ..., 0.047] We calculate the weight matrix for the layer for each token and for each attention head: Q = X * Wq heads K = X * Wk heads V = X * Wv heads where X is the sum vector for the token Wq, Wk, Wv are common and the same for all tokens in this layer, but different or partially different for each head For example: Wq heads = [[0.1, 0.2, 0.3], [0.4, 0.5, 0.6], [0.7, 0.8, 0.9], [1.0, 1.1, 1.2]] Wk heads = [[0.12, 0.22, 0.32], [0.42, 0.52, 0.62], [0.72, 0.82, 0.92], [1.02, 1.12, 1.22]] Wv heads = [[0.11, 0.21, 0.31], [0.41, 0.51, 0.61], [0.71, 0.81, 0.91], [1.01, 1.11, 1.21]] Then: Q "Hello" = x * Wq = [0.035, 0.207, 0.473, 0.047] * Wq Q[0] = 0.035 * 0.1 + 0.207 * 0.4 + 0.473 * 0.7 + 0.047 * 1.0 ≈ 0.0035 + 0.0828 + 0.3311 + 0.047 ≈ 0.4644 Q[1] = 0.035*0.2 + 0.207*0.5 + 0.473*0.8 + 0.047*1.1 = 0.007 + 0.1035 + 0.3784 + 0.0517 ≈ 0.5406 Q[2] = 0.035*0.3 + 0.207*0.6 + 0.473*0.9 + 0.047*1.2 = 0.0105 + 0.1242 + 0.4257 + 0.0564 ≈ 0.6168 Q = [0.4644, 0.5406, 0.6168] we calculate similarly for "Hello": K = [0.47964, 0.55684, 0.63204] V = [0.47299, 0.54822, 0.62442] and for other tokens
Calculating Attention Score between tokens:
At this point, we have Q, K, and V for one token and one attention head. Now we can move on to calculating attention score between tokens, for example, between “Hello” and “world”, using the formula:
In mathematical terms:
Q - matrix of Queries K - matrix of Keys V - matrix of Values d_k - vector dimension Attention(Q, K, V) = softmax((Q * Kᵀ) / √d_k + mask) * V Q * Kᵀ - matrix multiplication of Q by the transpose of K. This calculates the "raw" attention weights between each query and each key. √d_k - square root of the dimension of key vectors. Used for scaling to prevent softmax values from getting too large, which can lead to gradient problems. This is called Scaled Dot-Product Attention. mask is a matrix that is used to constrain attention. In generative models, a causal mask is used - it prevents a token from "seeing ahead" when computing attention. This is critical for problems where the model predicts the next token. softmax(...) - the softmax function is applied to the result of dividing Q ⋅ Kᵀ by √d_k (and adding mask if present). This normalizes the attention weights so that they sum to 1 for each query. Multiplying the softmax result by V yields a weighted sum of the values, where the weights are determined by the attention score.
Example:
Input:
| Token | Q-vector | K-vector | V-vector |
|----------|--------------------------|--------------------------|-----------------------|
| "Hello" | [0.4644, 0.5406, 0.6168] | [0.4796, 0.5568, 0.6320] | [0.473, 0.548, 0.624] |
|----------|--------------------------|--------------------------|-----------------------|
| "," | [0.2, 0.3, 0.1] | [0.25, 0.35, 0.15] | [0.12, 0.09, 0.04] |
|----------|--------------------------|--------------------------|-----------------------|
| "world" | [0.55, 0.33, 0.77] | [0.5213, 0.5967, 0.6721] | [0.55, 0.65, 0.75] |
For simplicity, we use the dimension d_k for Q, K = 3 (for example)
Calculation:
Hello–Hello: 0.4644*0.4796 + 0.5406*0.5568 + 0.6168*0.6320 ≈ 0.2228 + 0.3011 + 0.3899 = 0.9138
Hello–",": 0.4644*0.25 + 0.5406*0.35 + 0.6168*0.15 ≈ 0.1161 + 0.1892 + 0.0925 = 0.3978
Hello–world: 0.4644*0.5213 + 0.5406*0.5967 + 0.6168*0.6721 ≈ 0.2422 + 0.3225 + 0.4147 = 0.9794
","–Hello: 0.2*0.4796 + 0.3*0.5568 + 0.1*0.6320 ≈ 0.0959 + 0.1670 + 0.0632 = 0.3261
","–",": 0.2*0.25 + 0.3*0.35 + 0.1*0.15 = 0.05 + 0.105 + 0.015 = 0.17
","–world: 0.2*0.5213 + 0.3*0.5967 + 0.1*0.6721 ≈ 0.1043 + 0.1790 + 0.0672 = 0.3505
world–Hello: 0.55*0.4796 + 0.33*0.5568 + 0.77*0.6320 ≈ 0.2638 + 0.1837 + 0.4876 = 0.9351
world–",": 0.55*0.25 + 0.33*0.35 + 0.77*0.15 ≈ 0.1375 + 0.1155 + 0.1155 = 0.3685
world-world: 0.55*0.5213 + 0.33*0.5967 + 0.77*0.6721 ≈ 0.2867 + 0.1969 + 0.5185 = 1.0021
Divide by √d_k = √3 ≈ 1.732
| From \ To | Hello | "," | world |
|-----------|-------------------------|-------------------------|-------------------------|
| Hello | 0.9138 / 1.732 ≈ 0.5275 | 0.3978 / 1.732 ≈ 0.2296 | 0.9794 / 1.732 ≈ 0.5652 |
| "," | 0.3261 / 1.732 ≈ 0.1882 | 0.17 / 1.732 ≈ 0.0982 | 0.3505 / 1.732 ≈ 0.2023 |
| world | 0.9351 / 1.732 ≈ 0.5397 | 0.3685 / 1.732 ≈ 0.2127 | 1.0021 / 1.732 ≈ 0.5786 |
Apply the exponent for "Hello":
exp(0.5275) ≈ 1.694
exp(0.2296) ≈ 1.258
exp(0.5652) ≈ 1.759
Sum of all exponents for "Hello":
1.694 + 1.258 + 1.759 ≈ 4.711
softmax = exp(x) / sum of all exp(x)
Softmax weight for "Hello" relative to other tokens:
| Token | Softmax weight |
| ------ | -------------------- |
| Hello | 1.694 / 4.711 ≈ 0.36 |
| "," | 1.258 / 4.711 ≈ 0.27 |
| world | 1.759 / 4.711 ≈ 0.37 |
When "Hello" generates its representation (at the output of the attention layer), it:
takes 36% of the information from itself,
27% from ",",
and 37% from the word "world".
Weighted summation:
Output= 0.36 ∗ V("Hello") + 0.27 ∗ V(",") + 0.37 ∗ V("world")
Coordinate 1 = 0.36∗0.473+0.27∗0.12+0.37∗0.55≈0.1703+0.0324+0.2035 ≈ 0.4062
Coordinate 2 = 0.36∗0.548+0.27∗0.09+0.37∗0.65≈0.1973+0.0243+0.2405 ≈ 0.4621
Coordinate 3 = 0.36∗0.624+0.27∗0.04+0.37∗0.75≈0.2246+0.0108+0.2775 ≈ 0.5129
Attention Score for the token "Hello": [0.4062, 0.4621, 0.5129]This Attention Score vector is a new representation of the token “Hello”, which takes into account its context: both itself and its neighbors. These vectors are then either sent to the next attention layer or to the model output.
Comparing a token with itself is necessary because in self-attention each token “looks” at all tokens, including itself.
This is necessary in order to:
Save information about the token itself — otherwise it would be “lost” against the background of the others.
Learn to “enhance” or “suppress” yourself — for example, in some language situations the token is important in itself (for example, a personal pronoun), and sometimes its context is more important.
Ensure symmetry — the attention matrix is always square (n × n), and diagonally — this is just self-to-self attention.
Formally, attention is the weights by which a token aggregates information from other tokens (including itself) and w1 is the “Hello” attention to itself. If it were not counted, the “Hello” token would not participate in its own output at all.
Example:
He said he would come.
When the model processes the “he” token, it needs to:
“look” at other tokens — to understand the context,
but the “he” token itself is also important, so as not to lose information about who we are talking about.
Resources:
Wikipedia: Attention (machine learning)
Understanding Q,K,V In Transformer( Self Attention)
What is Query, Key, and Value (QKV) in the Transformer Architecture and Why Are They Used?
➤ Step 5: Head Concatenation, Concatenated Multi-Head Attention
The previous calculations were performed for each of the attention heads, now it is necessary to combine the results. Let me remind you that the results are different due to different Wq, Wk, Wv for different heads.
From a mathematical point of view:
h - number of heads of attention d_k - dimension of the Attention Score vector for each head AttentionScore_i - Attention Score vector for the i-th head. Concatenation (Combining vectors into one vector by coordinates): concat = [AttentionScore_1, AttentionScore_2, ..., AttentionScore_h]
Example:
Input data: Lets assume the dimension is 6 (2 heads × 3 values) Number of attention heads h = 2 Vector dimension d_k = 3 "Hello" for head 1 AttentionScore_1 = [0.4062, 0.4621, 0.5129] "Hello" for head 2 AttentionScore_2 = [0.22, 0.33, 0.44] Calculation: Concatenation (Combining vectors into one vector by coordinates): concat[0] = AttentionScore_1[0] = 0.4062 concat[1] = AttentionScore_1[1] = 0.4621 concat[2] = AttentionScore_1[2] = 0.5129 concat[3] = AttentionScore_2[0] = 0.22 concat[4] = AttentionScore_2[1] = 0.33 concat[5] = AttentionScore_2[2] = 0.44 concat = [0.4062, 0.4621, 0.5129, 0.22, 0.33, 0.44]
➤ Step 6: Output Projection (Wo)
After combining the attention outputs from different heads, they are typically passed through a Dense Layer to return them to the original model dimensional space.
In terms of mathematics:
concat ∈ ℝ⁶ - input vector
Wₒ ∈ ℝ⁶ˣ³ - projection weight matrix
output ∈ ℝ³ - output vector after projection
Multiplication:
output = concat • Wₒ
Detailed formula for each component of the output vector:
output[0] = concat[0]*W_o[0][0] + concat[1]*W_o[1][0] + concat[2]*W_o[2][0] + concat[3]*W_o[3][0] + concat[4]*W_o[4][0] + concat[5]*W_o[5][0]
Alternatively, as a sum:
output_j = ∑_{i=1}^{6} concat_i ⋅ W_o[i][j] for j = 1, 2, 3
Matrix:
output = concat (1x6) ⋅ W_o (6x3) = (1x3)Example:
Input data: Model dimension d_model = 3 This means that the projection matrix W_o will have dimension (6, 3), i.e. 6 inputs → 3 outputs W_o = [ [0.1, 0.2, 0.3], [0.0, 0.1, 0.0], [0.2, 0.0, 0.1], [0.1, 0.2, 0.2], [0.0, 0.1, 0.3], [0.3, 0.0, 0.1] ] Input vector after concat: concat = [0.4062, 0.4621, 0.5129, 0.22, 0.33, 0.44] Calculation: x = 0.4062*0.1 + 0.4621*0.0 + 0.5129*0.2 + 0.22*0.1 + 0.33*0.0 + 0.44*0.3 = 0.04062 + 0 + 0.10258 + 0.022 + 0 + 0.132 = 0.2972 y = 0.4062*0.2 + 0.4621*0.1 + 0.5129*0.0 + 0.22*0.2 + 0.33*0.1 + 0.44*0.0 = 0.08124 + 0.04621 + 0 + 0.044 + 0.033 + 0 = 0.2045 z = 0.4062*0.3 + 0.4621*0.0 + 0.5129*0.1 + 0.22*0.2 + 0.33*0.3 + 0.44*0.1 = 0.12186 + 0 + 0.05129 + 0.044 + 0.099 + 0.044 = 0.3602 Final output vector: output = [0.2972, 0.2045, 0.3602]
➤ Step 7: Adding Residual
this is the summation of the layer’s input to its output. We add the output to the input vector that was fed to the input of the block (input embedding or the output of the previous layer).
This is used to:
Preserve the original information (gradients are easier to pass back).
Avoid signal “fading” through many layers.
Make it easier to train even very deep neural networks.
Input data: Input vector input = [0.035, 0.207, 0.473] Output vector output = [0.2972, 0.2045, 0.3602] Calculation: residual = output + input = residual = [0.3322, 0.4115, 0.8332]
➤ Step 8: Layer Normalization
normalizes values within one feature vector, that is, by feature dimension.
Why do you need it:
Eliminates bias and large-scale differences between features.
Makes training more stable.
Accelerates neural network convergence.
Works better with small batches, unlike BatchNorm.
From a mathematical point of view:
Calculate the mean: μ = (1/n) * ∑ xₙ Calculate the standard deviation (std): σ = sqrt((1/n) * ∑ (xₙ - μ)^2 + ε) Where ε is a small number to avoid division by zero. Normalize each element: ̂xₙ = (xₙ - μ) / σ Optionally scale and shift (trainable parameters): yₙ = γ * ̂xₙ + β
Example:
Input data: x = [0.5972, 0.3045, 0.5602] Calculation: Calculate the mean: μ = (0.5972 + 0.3045 + 0.5602) / 3 = 1.4619 / 3 ≈ 0.4873 Calculate the standard deviation: σ = sqrt(((0.5972 - 0.4873)^2 + (0.3045 - 0.4873)^2 + (0.5602 - 0.4873)^2) / 3) = sqrt((0.0121 + 0.0334 + 0.0053) / 3) = sqrt(0.0169) ≈ 0.13 Normalize: ̂x₁ = (0.5972 - 0.4873) / 0.13 ≈ 0.845 ̂x₂ = (0.3045 - 0.4873) / 0.13 ≈ -1.405 ̂x₃ = (0.5602 - 0.4873) / 0.13 ≈ 0.561 After rounding and applying scaling and offset (if any): ≈ [0.87, -1.13, 0.26]
➤ Step 9: FFN (Feed-Forward Network) and MLP (Multilayer Perceptron):
FFN (Feed-Forward Network):
is a transformer component that processes each word (or token) individually, without regard to other tokens.
It is applied independently to each token after the attention layer and is a two-layer neural network with a non-linear activation function.
This allows the model to capture more complex dependencies.
MLP (Multilayer Perceptron):
is a type of neural network consisting of multiple fully connected layers neurons. In the context of LLM and transformers, MLP often means the same Feed-Forward Network (FFN).
MLP = general name of the architecture,
FFN = special case of MLP used inside transformers.
In terms of mathematics:
x - input vector of dimension d W1-weight matrix of the first linear layer of dimension (d_ff × d) b1-bias of the first layer of dimension d_ff W2-weight matrix of the second linear layer of dimension (d × d_ff) b2-bias of the second layer of dimension d f-activation function (e.g. ReLU or GELU) d-dimension of input/output d_ff-dimension of the hidden layer (usually d_ff = 4 × d) Basic formula of FFN: FFN(x) = W2 f(W1 x + b1) + b2 Stepwise decomposition: Linear transformation, dimension z1: (d_ff × 1): z1 = W1 x + b1 Nonlinear activation, applied elementwise, dimension is preserved: z2 = f(z1) Second linear transformation, the resulting vector is the same size as x: (d × 1): y = W2 z2 + b2
Example:
Input data: Hidden layer dimension d = 4, Internal dimension d_ff = 8, Activation: ReLU, Input vector: x = [x[0], x[1], x[2], x[3]] = [1.0, -2.0, 0.5, 3.0] 8x4 matrix W1 = [ [1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1], [1, 1, 1, 1], [1, -1, 1, -1], [0.5, 0.5, 0.5, 0.5], [-1, -1, -1, -1] ] Calculation: y[0] = 1 * x[0] + 0 * x[1] + 0 * x[2] + 0 * x[3] = 1.0 + 0 + 0 + 0 = 1.0 y[1] = 0 * x[0] + 1 * x[1] + 0 * x[2] + 0 * x[3] = 0 - 2.0 + 0 + 0 = -2.0 y[2] = 0 * x[0] + 0 * x[1] + 1 * x[2] + 0 * x[3] = 0 + 0 + 0.5 + 0 = 0.5 y[3] = 0 * x[0] + 0 * x[1] + 0 * x[2] + 1 * x[3] = 0 + 0 + 0 + 3.0 = 3.0 y[4] = 1 * x[0] + 1 * x[1] + 1 * x[2] + 1 * x[3] = 1.0 - 2.0 + 0.5 + 3.0 = 2.5 y[5] = 1 * x[0] + (-1) * x[1] + 1 * x[2] + (-1) * x[3] = 1.0 + 2.0 + 0.5 - 3.0 = 0.5 y[6] = 0.5 * x[0] + 0.5 * x[1] + 0.5 * x[2] + 0.5 * x[3] = 0.5 - 1.0 + 0.25 + 1.5 = 1.25 y[7] = -1 * x[0] + (-1) * x[1] + (-1) * x[2] + (-1) * x[3] = -1.0 + 2.0 - 0.5 - 3.0 = -2.5 Vector after the linear layer (before activation): y = [1.0, -2.0, 0.5, 3.0, 2.5, 0.5, 1.25, -2.5] Applying ReLU: ReLU(y[i]) = max(0, y[i]) ReLU(y) = [1.0, 0.0, 0.5, 3.0, 2.5, 0.5, 1.25, 0.0]
➤ Step 10: Residual + LayerNorm (second normalization layer):
After FFN, the input of this block (the result of step 6) is added to the result again and the vector is normalized again – this helps to preserve information and stabilize the calculations
➤ Step 11: Feeding the block output to the next transformer block:
Having received a normalized vector at the output of one transformer block, the model passes it to the input of the next block. There can be dozens of such blocks — each one adds more and more “understanding” of the context
➤ Step 12: Final LayerNorm normalization after the last block:
After the last layer, LayerNorm is applied again — this is the final touch before generating logits to smooth out the spread of values
➤ Step 13: Logits Projection + Softmax:
The normalized vector from the last layer is multiplied by the embedding matrix (or a separate linear layer) to obtain the raw scores (logits) for each token in the vocabulary. These estimates are then converted into probabilities using Softmax or directly fed into samplers for token selection.
What are logits:
“raw” values that have not yet been normalized into probabilities.
For example, if the dictionary consists of 50,000 tokens, then logits are simply 50,000 numbers, one for each token.
For each token in the sequence, the model has formed a representation (hidden state).
Now we need to convert this hidden state into logits for the dictionary – an estimate of the probability of each possible next token.
Linear Layer Transformation:
logits = hidden_state @ Wᵀ + b hidden_state: last vector (or whole sequence - but usually last token is of interest), Wᵀ: transposed matrix of embeddings (size [vocab_size, hidden_dim]), b: bias, often omitted for economy.
almost all modern LLMs use weight tying — that is, Wᵀ is taken from the same layer as the input embeddings. This saves memory and improves the generalization ability of the model.
➤ Step 14: Selecting the next token (sampling):
The resulting logits are passed through a chain of samplers: first, penalties for repetitions and temperature are applied, then filters (top-k, top-p, etc.), and finally the final sampler (mirostat, greedy selection or distribution). This token is added to the context, and the generation is repeated from step 1 until the end or the desired length is reached.
In the backend LLama.cpp you can create chains of samplers, first intermediate ones, then the chain should end with the final sampler.
The order of using samplers in llama.cpp:
1. Repeat penalties: - repeat_penalty - frequency_penalty - presence_penalty 2. Logit scaling: - temperature 3. Token filtering: - top_k - top_p - min_p - typical_p - tfs_z 4. Grammar restrictions: - grammar 5. Final token selection: - mirostat (v1 or v2) or - greedy / random sampling
Example from LLama.cpp (for developers):
// preparing chain parameters struct llama_sampler_chain_params sparams = llama_sampler_chain_default_params(); llama_sampler * smpl = llama_sampler_chain_init(sparams); // intermediate samplers: llama_sampler_chain_add(smpl, llama_sampler_init_top_k (50)); // Top-K llama_sampler_chain_add(smpl, llama_sampler_init_top_p (0.9f, 1)); // Top-P (nucleus) llama_sampler_chain_add(smpl, llama_sampler_init_min_p (0.8f, 1)); // Min-P llama_sampler_chain_add(smpl, llama_sampler_init_typical (0.95f, 1)); // Locally Typical llama_sampler_chain_add(smpl, llama_sampler_init_temp (0.7f)); //Temperature llama_sampler_chain_add(smpl, llama_sampler_init_temp_ext (0.7f, 0.1f, 1.5f)); // Extended temp llama_sampler_chain_add(smpl, llama_sampler_init_xtc (0.9f, 1.0f, 1, LLAMA_DEFAULT_SEED)); // XTC llama_sampler_chain_add(smpl, llama_sampler_init_top_n_sigma(1.5f)); // Top-nσ llama_sampler_chain_add(smpl, llama_sampler_init_grammar(vocab, grammar, "root")); llama_sampler_chain_add(smpl,llama_sampler_init_grammar_lazy_patterns(vocab, grammar, "root", patterns, 2, tokens, N)); // final sampler, only 1 option from: llama_sampler_chain_add(smpl, llama_sampler_init_mirostat(32000, LLAMA_DEFAULT_SEED, 5.0f, 0.1f, 100)); // Mirostat V1 llama_sampler_chain_add(smpl, llama_sampler_init_mirostat_v2(LLAMA_DEFAULT_SEED, 5.0f, 0.1f)); // Mirostat V2 llama_sampler_chain_add(smpl, llama_sampler_init_greedy()); // Greedy llama_sampler_chain_add(smpl, llama_sampler_init_dist(LLAMA_DEFAULT_SEED)); // Dist // after generation, do not forget to free the chain: llama_sampler_free(smpl);
Example of the sampler settings page from the application https://github.com/a-ghorbani/pocketpal-ai
➤ Intermediate samplers:
Temperature (temp):
controls the degree of randomness in choosing the next token from the probability distribution calculated by the model. Temperature narrows or widens the “choice funnel” of the next word. The lower it is, the narrower the funnel, the higher it is, the wider it is.
After the model has predicted the logits (raw probabilities) for all possible tokens, they are passed through a softmax function. Temperature affects this function:
P(token) = softmax(logits / temperature)
Effect of temperature parameter:
T = 1 logits are left as is.
T < 1 (e.g. 0.7) the model increases the differences between tokens – probable tokens become even more probable. Behavior becomes more predictable.
T > 1 (e.g. 1.5) the differences between tokens are smoothed out – the chance of choosing a less probable token increases. Behavior becomes more diverse and risky.
T → 0 softmax becomes argmax, and one most probable token is always chosen.
Initial logits: Token A: 3.0 Token B: 2.5 Token C: 1.0 After softmax without change (temp = 1.0): A: 64% B: 24% C: 12% With reduced temperature (temp = 0.5): A: 85% B: 13% C: 2% With increased temperature (temp = 1.5): A: 47% B: 31% C: 22%
Top-k:
the model selects the next token only from the k most probable ones. All other tokens are discarded, regardless of their absolute probability.
there are 6 tokens with the following probabilities: A: 0.35 B: 0.30 C: 0.15 D: 0.10 E: 0.06 F: 0.04 If top_k = 3, then we leave only: A: 0.35 B: 0.30 C: 0.15
Top-p (nucleus sampling):
the minimum set of tokens with the highest probabilities, the sum of which exceeds the specified threshold p, is selected. The remaining tokens are completely cut off, even if they had a high rank.
the model gave the token probabilities: A: 0.50 B: 0.25 C: 0.15 D: 0.08 E: 0.02 With min_p = 0.1, only: A, B, C D and E will be discarded, even if the total is now less than 1.0 - then the rest will be normalized.
Min-p:
all tokens with a probability lower than the specified threshold p are cut off. It severely restricts the selection by excluding tokens that are too unlikely regardless of their rank or the sum of their probabilities, as in top-p.
Typical sampling:
selects tokens that are close to the “typical” level of surprise, excluding those that are too predictable and too rare. Unlike top-k and top-p, it focuses on the median surprisal value rather than the probability of tokens.
Repetition penalties, Frequency penalty, Presence penalty:
reduces the chances of re-selection of already generated tokens by decreasing their logits. This helps to avoid annoying repetitions in the text and makes the output more diverse.
Logit bias:
a method that allows you to manually change the probability of individual tokens before applying softmax by adding or subtracting values from their logits. This gives fine-grained control: you can, for example, force the model to avoid certain words or, conversely, choose them more often.
Tail Free Sampling (TFS):
drops the long “tail” of the distribution, adjusting the probability density.
and others
➤ Final samplers:
Greedy:
the simplest generation method, in which the model always selects the token with the highest probability (maximum logit). It is fast and deterministic, but often leads to monotonous and predictable text.
Random:
the next token is chosen randomly, proportional to its probability after all samplers (top-k, top-p, etc.) have been applied. This is the opposite of greedy, which always takes the token with the highest probability.
Dist:
reduces the probability of tokens that form previously encountered n-grams to reduce text repetition. It dynamically penalizes repetitions, making the generation more diverse.
Mirostat v1:
maintains a given level of “surprise” (perplexity), dynamically adjusting the choice of words. It helps avoid excessive repetition (the boredom trap) and incoherence (the confusion trap), ensuring balanced and high-quality text generation.
Mirostat v2:
maintains a given level of surprise (perplexity) with more precise control than Mirostat v1. It uses an advanced feedback mechanism that allows dynamic adjustment of word choice to achieve consistent text quality.
Grammar:
uses grammar rules (usually in the form of CFG) to strictly constrain the allowed tokens at each generation step. Instead of changing the logits, it simply disallows all tokens that do not match the current legal state of the grammar, ensuring a strictly structured output.
and others
➤ Step 15. Iterate generation:
After the model selected the next token, it is added to the end of the input sequence.
The context is expanded: now all previous tokens plus the newly generated one are taken as the “source” text for tokenization.
The algorithm then returns to step 1 (tokenization), and the process is repeated until the termination conditions are met.
This loop allows you to build the entire output sequence one token at a time.
Termination conditions:
Generation ends when the model produces a special end-of-sentence (EOS) token or when a predefined maximum sequence length is reached.
This limitation prevents infinite or overly long responses.
Some implementations also add a probability threshold termination rule: if the maximum probability of the next token is below a given value, generation also stops.
➤ Step 16. Converting tokens to words:
Once the model has generated the required number of tokens, they are converted back into text – this is called detokenization. The tokenizer takes a sequence of numbers (tokens) and translates them into words and punctuation marks. Usually this is done after full generation or on the go, if you need to get the text “on the fly”.
TODO: there are many inaccuracies in the article, they will be corrected as soon as there is free time and desire
➤ Additional information:
➤ Launch methods (backends) for LLM models:
ONNX Runtime:
Cross-platform engine for running ONNX models.
File format: .onnx
TensorFlow (Inference API):
Standard engine for TensorFlow models, supports SavedModel and frozen graph.
Formats: SavedModel folder (saved_model.pb + variables/), single .pb file
TensorFlow Lite:
Lightweight engine for mobile and embedded devices, optimized for size and speed.
Format: .tflite
PyTorch (TorchScript):
Allows you to serialize and run models without depending on Python, with JIT optimizations.
Formats: .pt, .pth
NVIDIA TensorRT:
Hardware-accelerated engine for NVIDIA GPUs, compiles models (usually from ONNX) for a specific card.
Format: compiled engine .engine (or UFF/ONNX plan → .engine)
Intel OpenVINO:
Optimizes and accelerates networks on CPU and Intel GPU/VPU, converts models to IR format.
Formats: .xml (structure) + .bin (weights)
Apple Core ML:
Framework for running models on iOS/macOS, integrates with Xcode and is accelerated via Core ML Runtime.
Format:.mlmodel
Microsoft ML.NET:
.NET engine for inference on CPU, suitable for C# and F#.
Format: model archive .zip
Apache TVM:
Compiles and optimizes models for various hardware, creates native libraries.
Formats: serialized Relay module or compiled library (.so, .dll)
Alibaba MNN:
Mobile neural engine with extensive optimizations for ARM, supports server launch.
Format: .mnn
Tencent NCNN:
Compact engine for mobile CPU/GPU, no third-party dependencies.
Formats:.param (structure) + .bin (weights)
OpenCV DNN:
Computer vision module with support for various formats (ONNX, Caffe, TensorFlow, Darknet).
Formats: depends on the source — .onnx, .pb, .caffemodel + .prototxt, .weights
Unity Barracuda:
Engine for running neural networks in Unity games, supports ONNX models.
Format: .nn
MLC LLM:
ML compiler and engine for LLM, compiles weights into its IR and shards them.
Format: …-MLC directory with .bin shards and JSON configs (e.g. mlc-chat-config.json)
MediaPipe:
A framework for creating multimodal pipelines (detection, segmentation, etc.), based on TFLite.
Formats: .tflite (model) + .pbtxt (graph)
llama.cpp:
C++ engine for LLaMA-like models with CPU/GPU quantization support.
Formats: GGML models (.bin, .gguf)
GGML:
Library for efficient model inference (the basis of llama.cpp and others).
Formats: .gguf, .bin
NeuralMagic DeepSparse:
Optimized engine for sparse neural networks on CPU.
Format: .onnx
AWS Neuron SDK:
An engine for accelerating inference on AWS Inferentia, compiles models for Neuron.
Formats: Neuron artifacts (.nef or library)
Glow:
Facebook compiler and runtime for neural networks, ONNX input format.
Formats: intermediate .bc file or compiled .so library
Apache MXNet:
Framework with its own runtime for CPU/GPU, supports Docker deployment.
Formats: .params (weights) + .json (network)
Caffe:
Classic engine for CV networks, often used in research.
Formats: .caffemodel (weights) + .prototxt (network description)
➤ Applications for running LLM models:
LM Studio:
Desktop application for Windows and macOS with GUI for running local LLM (GPT-like).
Model formats: .gguf, .bin
Ollama:
Lightweight CLI/GUI client for Windows and macOS, works out of the box with LLM.
Model formats: .gguf, .bin
Automatic1111 Stable Diffusion WebUI:
The most popular local web interface for generating images on Windows/macOS/Linux.
Model formats:.ckpt, .safetensors
DiffusionBee:
Desktop application for macOS (there are beta builds for Windows), “all in one” for Stable Diffusion.
Model formats: .ckpt, .safetensors
InvokeAI:
Cross-platform package with CLI and WebUI for generating images based on Stable Diffusion.
Model formats: .ckpt, .safetensors
llama.cpp (prebuilt binaries):
Ready-made executables for Windows/macOS/Linux, allow you to run LLaMA-like models without installing dependencies.
Model formats: .bin, .gguf
➤ LLM models storage format:
.pt / .pth
Used in PyTorch to save trained models
Stores weights and model structure (or just weights).
Based on Python serialization (pickle), which makes them not very safe.
Suitable for training and retraining.
Not optimized for mobile inference or external inference
Can be memory intensive (FP32).
.safetensors
An alternative to .pt, a safe and fast format for PyTorch.
Does not use pickle, which means it is safe to load.
Supports parallel loading, which speeds up work.
Only for storing weights (structure is separate).
Suitable for inference and retraining.
Supports HuggingFace, PyTorch, JAX.
.bin
A general-purpose or proprietary binary format for model weights, especially in HuggingFace and old GGML.
Can be unformalized (structure depends on framework).
Can contain full weights or quantized data.
Suitable for loading into custom engines (e.g. llama.cpp).
Requires precise knowledge of how to interpret the contents.
Often used in legacy projects or custom pipelines.
.gguf
New standard from GGML for running LLM in llama.cpp, Ollama, MLC LLM.
Includes everything in one file: weights, dictionary, tokenizer, model parameters.
Supports different types of quantization (Q2_K, Q4_0, Q8_1, etc.).
Well compressed and optimized for running on CPU, GPU, Android.
Fast loading and easy to process by C++ code.
The main choice for local LLM running (Gemma, LLaMA, Mistral).
.onnx
Cross-framework format for running models in different environments (Windows, Web, C#, Java, etc.).
Standardized, supported by many frameworks (PyTorch, TF, Keras).
Simplifies the transfer of models between platforms.
Suitable for inference (not for training).
Optimized by ONNX Runtime (compression, quantization).
An excellent choice for running models in embedded environments and .NET.
.tflite
Format for running TensorFlow models on mobile devices (Android, iOS).
Very compact and fast.
Supports INT8 and FP16 quantization.
Works with TensorFlow Lite Interpreter, easily integrated into Android.
Cannot train or retrain – only run.
Supports basic CNN, RNN, Seq2Seq, but not LLM.
.mlc
Format for MLC LLM – LLM run on Android/iOS/GPU via compilation.
The model is pre-compiled into efficient bytecode.
Supports Vulkan/Metal/OpenCL for acceleration.
Used for Gemma, Mistral, LLaMA on phone.
Requires complex preparation (TVM, scripts, setup).
Great for mobile applications without servers.